Huffman Encoding Algorithm
Data transmission is essential for the proper functioning of any structure on any level and any type of organisation. The faster data are transmitted, the smoother the structure operates. There are generally two ways to make data transmission fast: by improving the means of transfer or by changing the data so that the same information can be sent within a shorter time interval. In this tutorial, I am going to explore the Huffman Encoding algorithm used for doing data compression. It is one of the essential algorithms behind file or text compression.
We are going to learn how the Huffman Encoding (or Coding) works and implement it in C++.
- Principle of Huffman Encoding algorithm
- Pseudo code algorithm
- Work through an example
- Implementation in C++
- Complexity
- Applications
Principle of Huffman Encoding algorithm
Huffman’s algorithm is based on the construction of a binary tree that represents the code. Let T be that binary tree. Each node in T except the root represents a bit(0 or 1) in the code. A left child is represented by a 0 and a right child is reprensented by a 1. Each disctinct caracter is then represented by an external node w. The code word for a caracter is obtained by concataining the bits associated with each node on the path from the root of the tree to w. Since each caracter is associated with its occurence. Then each node of T has a frequency associated. The frequency of an external node w is the frequency of the caracter associated and the frequency of an internal node u is the sum of the frequency of all external nodes in the subtree rooted at u.
Pseudo code algorithm
Algorithm: Huffman(X)
input: String X of length n with d distinct caracters
output: Huffman Coding tree of X
Compute the occurence f(c) of each caractere
Create an empty priorty queue q
For each caracter c in X do:
Create a single-node binary tree T storing c
Insert T into q with key f(c)
While q.size() > 1 do:
c1 <-- q.min()
t1 <-- q.removeMin()
c2 <-- q.min()
t2 <-- q.removeMin()
Merge t1 and t2 into a new tree t with t1 left child and t2 right child
Insert t into q with key equals to c1+c2
return q.removeMin()
The Huffman coding algorithm pseudo-code
Work through an example
Let’s see an example of the Huffman code for the input string
S = “Better to arrive late than not to come at all”
1: First, we compute the frequency of each character in S . Then we should obtain the table below.
| Character | empty character | a | b | c | e | h | i | l | m | n | o | r | t | v |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Frequency | 9 | 5 | 1 | 1 | 5 | 1 | 1 | 3 | 1 | 2 | 4 | 3 | 8 | 1 |
2: Second, we run the huffman encoding algorithm described above to create the Huffman tree.
I used a Huffman Coding algorithm visualisation tool built by Yves Lucet available here.
Watch the visualisation below which described step by step how the algorithm works.
Visualisation of the Huffman Encoding algorithm
Here is the Huffman Coding tree for the string “Better to arrive late than not to come at all”.
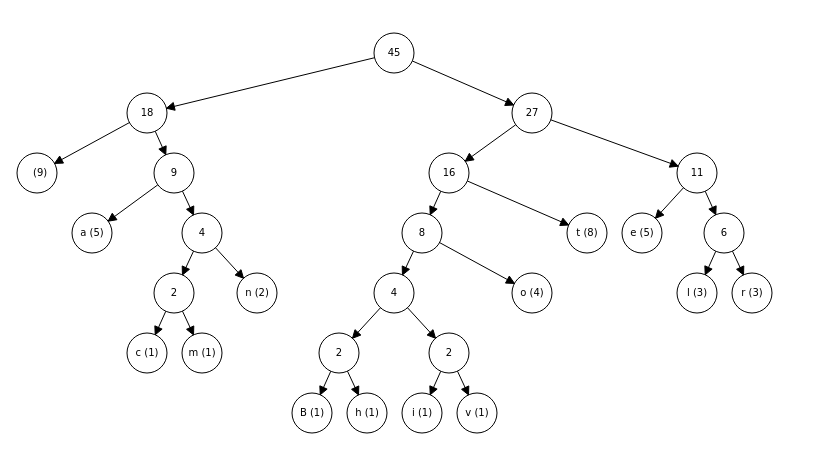
Huffman Encoding Tree
In the Huffman tree, a left child is represented by a 0 and a right child is represented by a 1. So we can compute now the binary code for each caracter in the input string.
| Character | empty character | a | B | c | e | h | i | l | m | n | o | r | t | v |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Encoding | 00 | 010 | 100000 | 01100 | 110 | 100001 | 100010 | 1110 | 01101 | 0111 | 1001 | 1111 | 101 | 100011 |
Implementation in C++
// file: "huffman_coding.h"
#ifndef HUFFMAN_CODING_H
#define HUFFMAN_CODING_H
#include<iostream>
#include<queue>
#include <map>
using namespace std;
class Node
{
public:
int frequency;
char caracter;
Node* leftNode;
Node* rightNode;
};
#define MAX_ARR 100
class Huffman {
private:
map<char,int> computeFrequencies(string text);
Node* huffman_coding_tree(string text);
void printHuffmanCode(Node* tree, int (&arr)[MAX_ARR], int size, string & encoding);
public:
string huffmanEncoding(string text);
};
#endif HUFFMAN_CODING_H
// file: "huffman_coding.cpp"
#include "huffman_coding.h"
int main(){
string text = "Better to arrive late than not to come at all";
string encoding = Huffman().huffmanEncoding(text);
cout << encoding << endl;
}
map<char, int> Huffman::computeFrequencies(string text) {
map<char, int> counter;
for (char c: text) {
if (counter.find(c) == counter.end()) {
counter[c] = 0;
}
counter[c] += 1;
}
return counter;
}
Node* Huffman::huffman_coding_tree(string text){
map<char,int> counter = computeFrequencies(text);
priority_queue<pair<int, Node*>> min_heap;
for(auto item: counter){
Node* caracterNode = new Node();
caracterNode->frequency = item.second;
caracterNode->caracter = item.first;
min_heap.push(make_pair(-1*item.second, caracterNode));
}
while (min_heap.size() > 1){
pair<int, Node*> leftNode = min_heap.top();
min_heap.pop();
pair<int, Node*> rightNode = min_heap.top();
min_heap.pop();
Node* node = new Node();
node->frequency = leftNode.second->frequency + rightNode.second->frequency;
node->leftNode = leftNode.second;
node->rightNode = rightNode.second;
min_heap.push(make_pair(-1*node->frequency, node));
}
return min_heap.top().second;
}
string Huffman::huffmanEncoding(string text){
Node* tree = huffman_coding_tree(text);
string encoding = "";
int arr[MAX_ARR];
int top = 0;
for(int i = 0; i < MAX_ARR; i++){
arr[i] = 0;
}
printHuffmanCode(tree, arr, top, encoding);
return encoding;
}
void Huffman::printHuffmanCode(Node* tree, int (&arr)[MAX_ARR], int size, string & encoding){
if(tree == 0) return;
if(tree->leftNode != 0) {
arr[size] = 0;
printHuffmanCode(tree->leftNode, arr, ++size, encoding);
}
if(tree->rightNode != 0) {
arr[size] = 1;
printHuffmanCode(tree->rightNode, arr, ++size, encoding);
}
if(tree->rightNode == 0 && tree->leftNode == 0){
string s(1, tree->caracter);
encoding += s + " | " ;
for (int i = 0; i < size; i++){
encoding += to_string(arr[i]) + " ";
}
}
}
Complexity
The Huffman Coding algorithm create an optimal code for a string of length n with d distinct characters in O(n+dlogd) time.
Applications
Text compression is an important text processing task. It is useful in any situation where we are communicating over a low-bandwidth channel, such as a modem line or infrared connection or IoT, and we wish to minimize the time needed to transmit our text. Likewise, text compression is also useful for storing collections of large documents more efficiently, in order to allow for a fixed-capacity storage device to contain as many documents as possible. Today, the Huffman Coding is used to design text editors and many other text processing applications. It is also behind the compression algorithms used by tools like Microsoft Word and a bunch of other text editors. The Huffman Coding is the algorithm behind the design of many compressions algorithms like GZIP, BZIP2, PKZIP.
Thanks for reading. I hope you found this tutorial helpful and I would love to hear your feedback in the Comments section below . You can also share with me what you have learned by sharing your creative projects with me.
