Algorithm time complexity (Basics)
The efficiency of algorithms is important in programming. Often, it is easy to come up with an algorithm that solves the problem by using brute force solution . That kind of solution is most of the time very expensive to run because it requires lot of computing power (ram, cpu or gpu). The real challenge when designing an algorithm is to design a fast one that requires less computing power and solves the problem in the shortest time.
Definition
In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Source Wikipedia
Rules
Notation
The time complexity of an algorithm is denoted O(f(n)) where f(n) represents some function. Often n denotes the input size. For instance :
- if the input is an array of numbers, n will be the size of the array
- if the inpout is a string, n will be the lenght of the string
f(n) represents the number of elementary operations(addition/substraction, multiplication, division)
A common reason why an algorithm takes a lot of computing power is that it contains a lot of loops. The more nested loop the algorithm depends on, the slower it is. For instance, if an algorithm use k nested loops and in each loop, it iterates over an input of size n, the time complexity will be O(n**k).
Examples: The time complexity of the following code is O(n) because we have one loop that iterates over an input of size n and for each element of the input, it does one elementary operation(addition).
for(int i = 1; i <= n; i++){
answer += 1 + i;
}
The time complexity of the following code is O(n*2) because we have two nested loop and each loop iterates over an input of size n.
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
answer += i + j;
}
}
Order of magnitude
A time complexity does not tell us the exact number of elementary operations that a code does to solve a problem but it shows only the order of magnitude. It is an approximative evaluation of the maximum number of computing operations required to solve a problem.
Exemple 1: In the following code, the loop is executed 5 times over an input of size n. For every element of the input, it does some elementary computing operations . Those operations requires are said to ran in constant time. Let be c the constant number of elementary operations inside the loop. So the time complexity of this code is O(5nc) which is equivalent to O(n). O(5nc) ~ O(n)
for(int i = 1; i <= 5*n; i++){
answer += 1 + i;
answer += i*10;
answer *= i*15;
// more elementary computing operations below
}
Exemple 2: In the following code, the loop is executed one time over an input of size n + 15. For every element of the input, it does some elementary computing operations . Those operations requires are said to ran in constant time . Let be c the constant number of elementary operations inside the loop. So the time complexity is O((n+15)c) which is equivalent to 0(n+15) also equivalent to O(n). O((n+15)c) ~ 0(n).
for(int i = 1; i <= n+15; i++){
answer += 1 + i;
answer += i*10;
answer *= i*15;
// more elementary computing operations below
}
Basic complexity classes
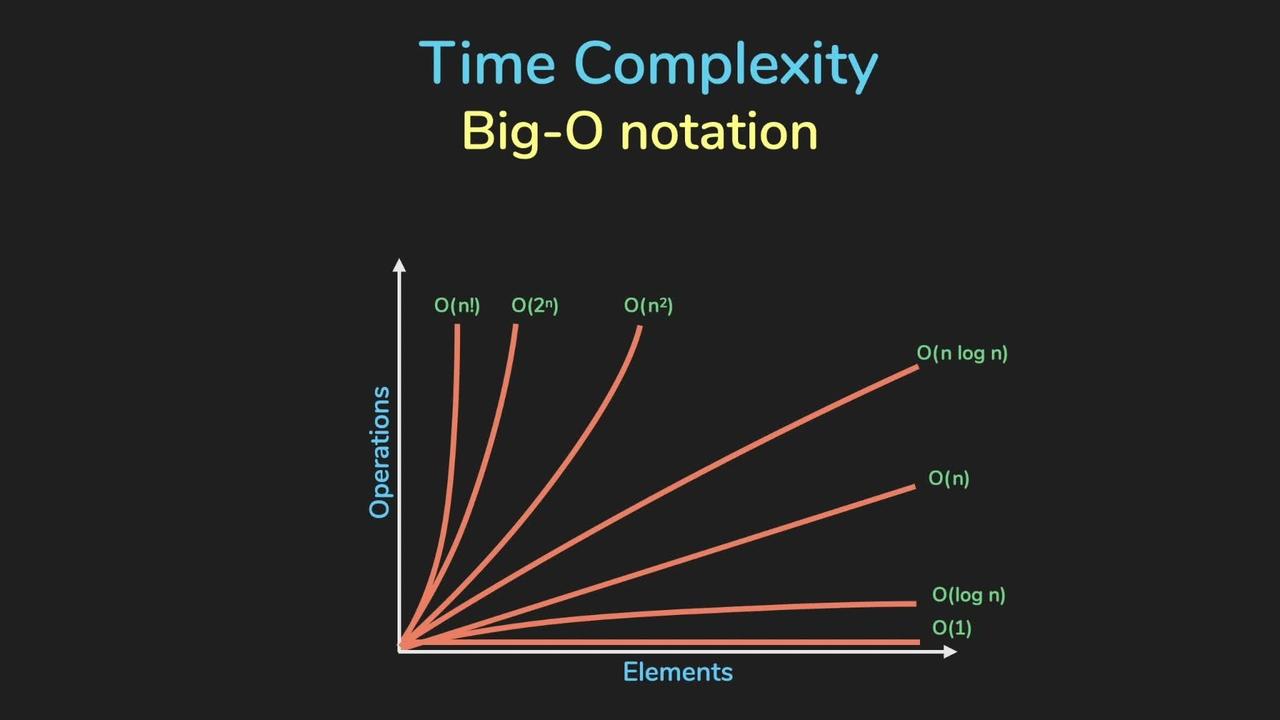
O(1) The running time of a constant-time algorithm does not depend on the input size. A typical constant-time algorithm is a direct formula that calculates the answer.
O(log(n)) A logarithmic algorithm often halves the input size at each step. The running time of such an algorithm is logarithmic, because log base 2 of n equals the number of times n must be divided by 2 to get 1.
O(square_root(n)) A square root algorithm is slower than O(log(n)) but faster than O(n).
O(n) An algorithm that goes through the input a constant number of times. It is called a linear algorithm
O(nlog(n)) This time complexity often indicates that the algorithm sorts the input, because the time complexity of efficient sorting algorithms O(nlog(n). Another possibility is that the algorithm uses a data structure where each operation takes O(log(n)) time.
In the following article (Time complexity (Part two)), I will explain more about time complexities phases and estimation.
